Регрессия Matlab | Как выполнить регрессию данных в Matlab

Регрессия — это статистический метод, используемый для моделирования взаимосвязи между зависимой переменной и одной или несколькими независимыми переменными. Зависимая переменная — это ответная переменная, а независимые переменные — предикторные переменные. Регрессия — это мощный инструмент, который можно использовать для понимания взаимосвязей между переменными, составления прогнозов и проверки гипотез.

Цель этого блога — познакомить читателя с основами регрессии в Matlab. Мы начнем с обсуждения различных типов регрессии, а затем покажем, как выполнить регрессионный анализ в Matlab.

Станьте экспертом в области науки о данных и получите работу своей мечтыПрограмма аспирантуры Калифорнийского технологического института по науке о данныхИзучить программу

Введение в регрессию Matlab

Регрессия MATLAB — это функция, используемая для поиска линейной связи между двумя или более переменными. Одна переменная рассматривается как объясняющая переменная, в то время как вторая переменная рассматривается как зависимая переменная. Это непрерывная переменная по своей природе. Зависимая переменная — это термин, используемый для описания переменных, значения которых анализируются или фокусируются, в то время как независимая или объясняющая переменная концентрируется на зависимой переменной. В случае зависимых переменных она обозначается как Y, в то время как объясняющие или независимые переменные обозначаются как X. Для выполнения многолинейного регрессионного анализа отклика в матрице объясняющих переменных на предикторы матрицы независимой переменной используется функция регрессии Matlab.

Это можно использовать для поиска линии наилучшего соответствия для разбросанных данных. Данные не обязательно должны быть идеально линейными, но они должны быть близки. Используя этот метод, можно также вычислить уравнение линии наилучшего соответствия. Регрессия Matlab — это метод подгонки кривой к точкам данных, чтобы кривую можно было использовать для прогнозирования будущих значений. Регрессия Matlab — это мощный инструмент, который можно использовать для поиска тенденций в наборах данных, которые в противном случае было бы трудно обнаружить.

Как работает регрессия в Matlab?

Регрессионный анализ исследует связь между двумя переменными. В Matlab регрессию можно выполнить с помощью встроенной функции регрессии. Эта функция принимает два вектора, зависимую переменную и независимую переменную, и выводит вектор коэффициентов регрессии. Затем эти коэффициенты можно использовать для подгонки линии к данным.

Чтобы понять, как функционирует функция регрессии с использованием Matlab, выполните следующие простые шаги:

• Шаг 1. Установите одну переменную в качестве объяснения или независимой переменной и загрузите все входные данные.
• Шаг 2. Добавьте еще одну переменную в качестве зависимой и загрузите все данные.
• Шаг 3. Запишите уравнение, которое может включать крутизну линии.
• Шаг 4. Затем вы можете использовать функцию регрессии MATLAB, используя правильный синтаксис.
• Шаг 5. Используйте программу MatLab для генерации выходных данных.

Линейная и полиномиальная регрессия

В линейной регрессии одна или несколько переменных-предикторов используются для прогнозирования непрерывной переменной результата на основе одной или нескольких переменных-предикторов. Переменная результата является постоянной, поскольку она может принимать любое значение в пределах диапазона (например, доход, рост, вес и т. д.). Предикторы могут быть непрерывными или категориальными (например, возраст, пол, раса и т. д.).

Полиномиальная регрессия — это обобщение линейной регрессии, позволяющее прогнозировать непрерывную переменную результата на основе одной или нескольких переменных-предикторов. Однако, в отличие от линейной регрессии, полиномиальная регрессия может моделировать нелинейные связи между переменными-предикторами и результатами.

Оба метода находят наилучшую линию или кривую для набора точек данных. Основное различие между ними заключается в типе кривой, подобранной к данным. Линейная регрессия создает прямую линию, тогда как полиномиальная регрессия создает кривую линию.

Регрессия по линейному уравнению является самым простым из двух методов и обычно является первым выбором при прогнозировании будущих значений. Однако, если связь между зависимыми и независимыми переменными нелинейна, то полиномиальная регрессия может быть лучшим выбором.

Нелинейная регрессия с APM Matlab

APM Matlab — мощный инструмент для нелинейного регрессионного анализа. Он может подгонять нелинейные модели к данным с несколькими предикторными переменными. В этом разделе ниже вы узнаете, как использовать APM Matlab для нелинейной регрессии.

Сначала вам нужно будет загрузить данные в APM Matlab. Для этого откройте файл данных в APM Matlab и выберите опцию «Нелинейная регрессия» в меню «Анализ». Затем выберите опцию «Переменные-предикторы» и выберите переменные-предикторы, которые вы хотите использовать в модели. Наконец, выберите «Зависимая переменная» и выберите переменную, которую вы хотите предсказать.

После загрузки данных вам нужно будет указать тип модели, которую вы хотите использовать. APM Matlab предлагает множество различных видов моделей, включая линейные, полиномиальные, экспоненциальные и логистические модели. Вы также можете указать количество переменных-предикторов, которые вы хотите использовать в модели.

После указания типа модели вам необходимо оценить параметры модели. Для этого выберите кнопку «Оценить» в меню «Анализ». APM Matlab оценит параметры модели, используя загруженные вами данные.

После оценки параметров модели вы можете использовать функцию «predict» для прогнозирования новых значений зависимой переменной. Для этого выберите кнопку «Predict» в меню «Analysis» и введите значения переменных-предикторов, которые вы хотите использовать в прогнозе. Затем APM Matlab предскажет значение зависимой переменной для каждого значения введенных вами переменных-предикторов.

Станьте экспертом в области науки о данных и получите работу своей мечтыПрограмма аспирантуры Калифорнийского технологического института по науке о данныхИзучить программу

Примеры регрессии Matlab

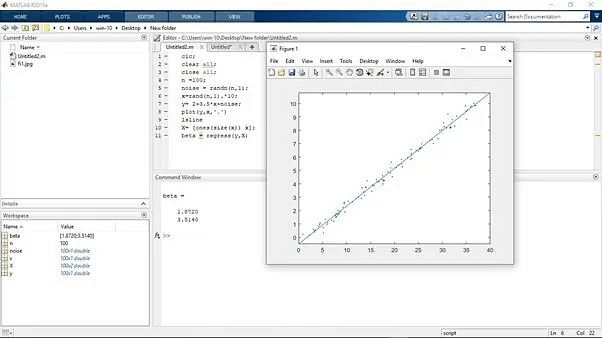
Давайте рассмотрим пример, иллюстрирующий регрессию Matlab, и посмотрим, как она работает в Matlab. Поскольку мы знаем о процедуре регрессии Matlab, мы использовали функцию MATLAB для регрессии Matlab. Допустим, количество наблюдений равно 100. Затем мы создаем искусственный шум с помощью функции rand. “noise is randn(n,1);” эта строка используется для создания искусственного звука. После этого мы создаем независимую переменную “x. “x=rand(n,1). *10” Эта строка является источником независимой переменной x, искусственно увеличенной по сравнению с шумом.

После этого мы готовы создать уравнение. “y= 2+3.5*x+noise;” эта последовательность является уравнением. Здесь наклон для независимой переменной x равен 3.5. Мы также добавляем искусственный шум к этому уравнению. Затем мы строим график, используя функцию plot между независимой переменной x и зависимой переменной y. Затем мы используем синтаксис “lsline”, чтобы нарисовать контур и построить его. После этого мы строим бета-значения, которые мы сначала создали, соединяя единицы. Используя “X= (ones(size(x)) *x”;” Эта линия используется для создания начальных бета-значений, и, наконец, мы генерируем окончательную бету, используя эту функцию регрессии MATLAB. “beta = regress(y,X)” Это заданное уравнение генерирует бету. После выполнения кода Matlab мы получим два бета-значения.

Код:

Выход:

Часто задаваемые вопросы

1. Можно ли выполнить регрессию в Matlab?

Да, вы можете делать регрессию в Matlab. Matlab имеет несколько встроенных функций, которые упрощают подгонку линейных и нелинейных моделей к данным. Вы также можете использовать Matlab для настройки своих алгоритмов регрессии.

2. Что такое регрессионный анализ в Matlab?

Цель регрессионного анализа — исследовать взаимосвязи между различными переменными. Он может предсказывать будущие события или поведение, понимать, как различные факторы влияют друг на друга, или выявлять тенденции или закономерности.

3. Как выполнить простую линейную регрессию в Matlab?

В Matlab есть много способов сделать линейную регрессию. Самый простой способ — использовать функцию fitlm, которая автоматически подгонит линейную модель под ваши данные. Вы также можете использовать функцию polyfit, чтобы подгонять полиномиальную модель под ваши данные. Если вам нужен больший контроль над процессом подгонки, вы можете использовать функцию lsqlin.

4. Что такое lm в Matlab?

Класс LinearModel в Matlab предлагает набор функций, которые упрощают подгонку линейных моделей к данным. Линейные модели — это тип математической модели, которая может описывать широкий спектр физических явлений. В общем случае линейная модель — это любое уравнение, которое можно записать:

у = мх + б

Где y = зависимая переменная, m = наклон линии, x = независимая переменная, и b = отсекаемый отрезок. Класс линейных моделей предлагает множество функций для подгонки линейных моделей к данным, включая функции для оценки наклона и отсекаемого отрезка, вычисления прогнозов и расчета доверительных интервалов.

5. Что такое линейная регрессия в MATLAB?

Метод линейной регрессии используется для поиска линейной связи между двумя переменными. Другими словами, он помогает нам понять, как одна переменная изменяется по отношению к другой. Линейная регрессия — это мощный инструмент, используемый для прогнозирования, и часто применяется в таких областях, как инженерия, финансы и статистика.

6. Как делать прогнозы в MATLAB?

В MATLAB есть несколько способов прогнозирования будущих значений. Наиболее распространенный метод — использование линейной регрессии, которая является наилучшей линией соответствия для набора данных. Затем мы можем прогнозировать будущие значения. Другие методы прогнозирования включают использование полиномиальной регрессии или нейронной сети.

Заключение

Регрессия Matlab — мощный инструмент для анализа данных. Он прост в использовании и может предоставить информацию, которую было бы трудно получить с помощью других методов. В этой статье кратко описывается регрессия Matlab и ее использование для регрессии данных. Зарегистрируйтесь в Caltech Data Science Bootcamp, чтобы узнать больше о регрессии данных.